--- title: Deriving the Universal Surge Curve description: "A description of how the \"Universal Surge Curve\" is derived" --- [![26TRIS065-Tri-Sen 50 years logo-R2](https://blog.tri-sen.com/hs-fs/hubfs/Assets/26TRIS065-Tri-Sen%2050%20years%20logo-R2.png?width=1476&height=573&name=26TRIS065-Tri-Sen%2050%20years%20logo-R2.png "26TRIS065-Tri-Sen 50 years logo-R2")](https://tri-sen.com/) # Tri-Sen Blog # Deriving the Universal Surge Curve By [Jim Jacoby](https://blog.tri-sen.com/author/jim-jacoby) on Jan 6, 2020 11:37:39 AM ![Jim Jacoby](https://blog.tri-sen.com/hubfs/Jim%20blog%20author.jpg) Share this post - [Tweet](https://twitter.com/share) In this post we will describe how we can convert a compressor manufacturer's compressor performance map to a surge line we can use to determine where, in relation to that surge line, a compressor is operating. Compressor manufacturers present their performance maps as the polytropic head vs. the inlet volumetric flow. 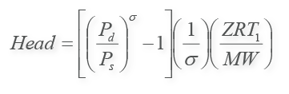The polytropic head can be expressed with the following equation:  ![head equation](https://blog.tri-sen.com/hs-fs/hubfs/head%20equation.png?width=289&name=head%20equation.png)     Where: Pd = compressor discharge pressure Ps = compressor suction pressure σ = polytropic exponent    = (k-1)/kη k = specific heat ratio η = compressor polytropic efficiency Z = compressibility at suction conditions R = universal gas constant T1 = compressor suction temperature MW = molecular weight of gas The inlet volumetric flow can be expressed with the following equation: ![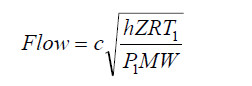flow equation](https://blog.tri-sen.com/hs-fs/hubfs/flow%20equation.jpg?width=252&name=flow%20equation.jpg) Where: c = flow coefficient of flow meter h = differential pressure across flow meter One objective in the development of a surge line prediction algorithm is to simplify these equations if possible. In the forms shown above, no simplification is possible. But if the flow equation is squared, several of the gas terms will cancel out. The next two figures depict a performance map for a single stage centrifugal compressor. The surge curve for a single stage compressor is a parabola [Head = f(Flow2)].   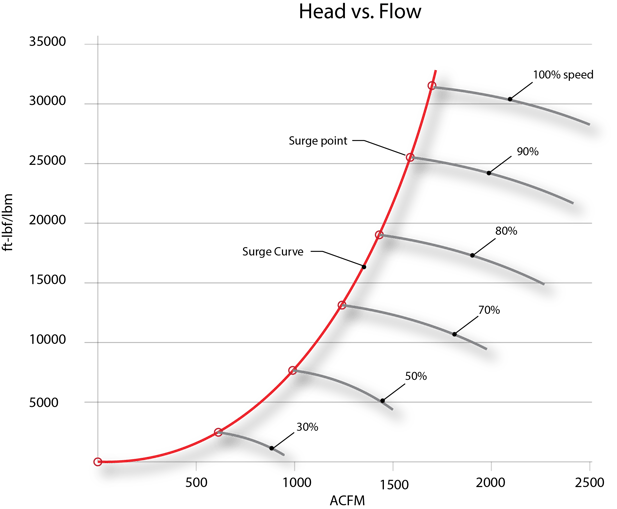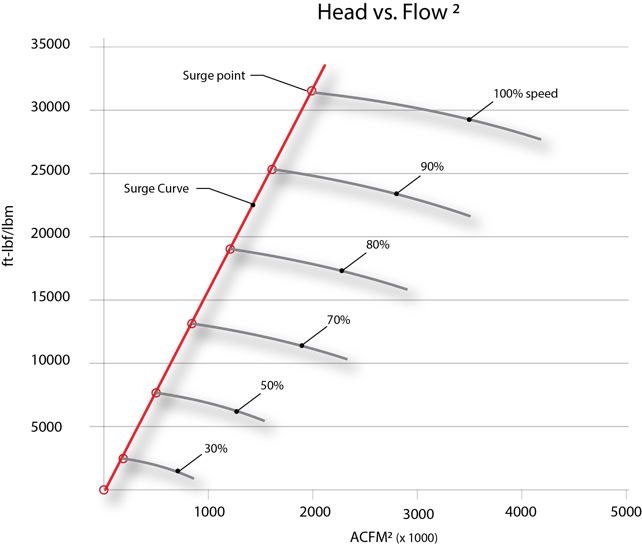![head vs flow](https://blog.tri-sen.com/hs-fs/hubfs/blog/blog%20-%20universal%20surge%20curve/head%20vs%20flow.png?width=617&name=head%20vs%20flow.png) *Figure 1 - performance map for a single stage centrifugal compressor*       ![head vs flow^2](https://blog.tri-sen.com/hs-fs/hubfs/blog/blog%20-%20universal%20surge%20curve/head%20vs%20flow%5E2.png?width=642&name=head%20vs%20flow%5E2.png) > *Figure 2 -  If the compressor capacity map (from figure 1) is plotted as Head vs. **Flow2** the surge curve is linear*   When the compressor curve is expressed in terms of the head vs. the flow squared, it is possible to see how the algorithm will reliably predict the surge line even if the gas (molecular weight) changes.   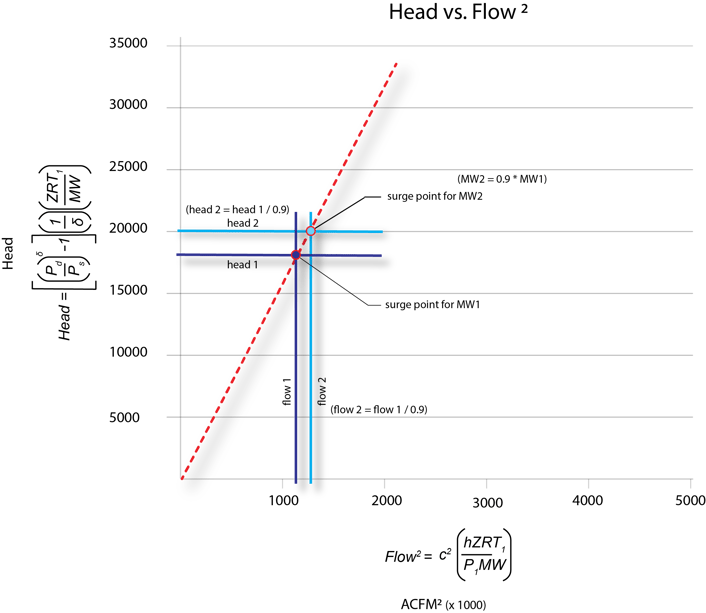![universal surge calc](https://blog.tri-sen.com/hs-fs/hubfs/blog/Blog%20-%20Deriving%20Universal%20Surge%20Curve/universal%20surge%20calc.png?width=706&name=universal%20surge%20calc.png) > *Figure 3 – When the surge line is expressed in terms of the head vs. flow squared, any changes* > *to the molecular weight will affect the head term in the same way that it affects the flow term. So* > *if the molecular weight drops by 10%, the head will increase by 11% and the flow will also* > *increase by 11% (1/0.9). 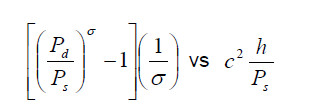The new surge point will fall on the same line.*   By cancelling like terms between the head equation and the flow squared equation, the surge line algorithm reduces to: ![simplified surge line algorithm](https://blog.tri-sen.com/hs-fs/hubfs/simplified%20surge%20line%20algorithm.jpg?width=332&name=simplified%20surge%20line%20algorithm.jpg) The polytropic exponent can be treated as a constant since the specific heat ratio tends to change very little and the efficiency is constant along the surge line (see figure 5 below). The flow meter coefficient is a constant, as well. 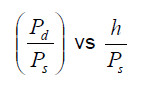This reduces the surge line algorithm to ![simplified surge line algorithm (2)](https://blog.tri-sen.com/hs-fs/hubfs/simplified%20surge%20line%20algorithm%20(2).jpg?width=181&name=simplified%20surge%20line%20algorithm%20(2).jpg) If the origin of the map is moved up to a y intercept of 1, the algorithm reduces to: ![final simplified surge algorithm](https://blog.tri-sen.com/hs-fs/hubfs/final%20simplified%20surge%20algorithm.jpg?width=159&name=final%20simplified%20surge%20algorithm.jpg)   ![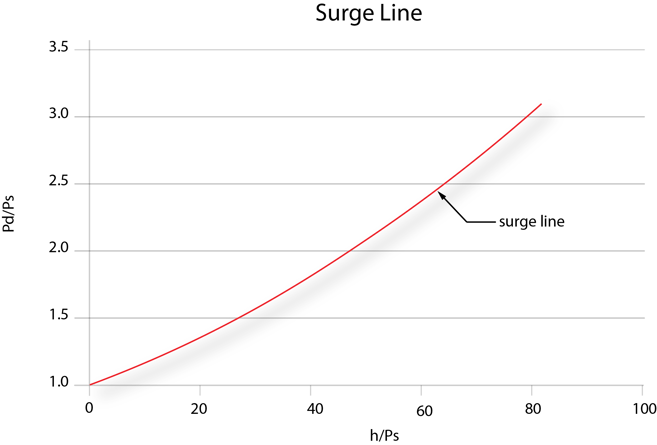surge line](https://blog.tri-sen.com/hs-fs/hubfs/blog/blog%20-%20universal%20surge%20curve/surge%20line.png?width=657&name=surge%20line.png) > *Figure 4 – the surge line of the compressor shown in figure 1 becomes the above curve when* > *our surge curve algorithm is applied.*    **Efficiency curves** – in this example, there is a change in the efficiency at the surge line over the entire speed range of less than 7%. In the speed range from 70% to 100% (normal speed range), the deviation is only about ½%. For predicting the surge line, the efficiency can be assumed constant. 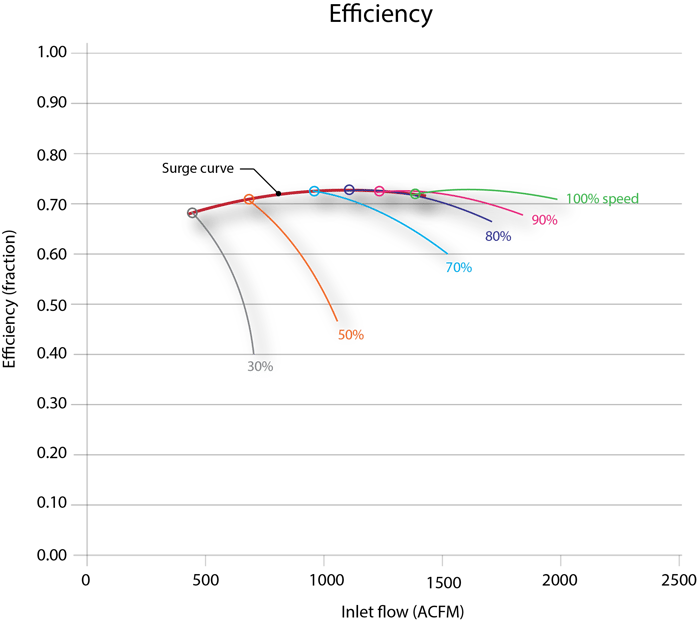![efficiency curve](https://blog.tri-sen.com/hs-fs/hubfs/blog/Blog%20-%20Deriving%20Universal%20Surge%20Curve/efficiency%20curve.png?width=697&name=efficiency%20curve.png) > ### *Figure 5 – Efficiency curves*   Topics [ compressor control ](https://blog.tri-sen.com/topic/compressor-control) , [ surge ](https://blog.tri-sen.com/topic/surge) , [ process protection ](https://blog.tri-sen.com/topic/process-protection) , [ recycle ](https://blog.tri-sen.com/topic/recycle) , [ compressor efficiency ](https://blog.tri-sen.com/topic/compressor-efficiency) , [ polytropic ](https://blog.tri-sen.com/topic/polytropic) , [ surge curve ](https://blog.tri-sen.com/topic/surge-curve) #  The Tri-Sen Blog... About once every two weeks, we'll discuss a turbomachinery controls related topic that  we were either asked about recently or a topic that we think you might be interested in learning more about.  Topics that are included or that will be: - Compressor Controls - Turbine Controls - Turbine Safety - Relevant API directives - General Industry happenings ### Subscribe Here! ### Recent Posts ### Posts by Tag - [compressor control (10)](https://blog.tri-sen.com/tag/compressor-control) - [surge (9)](https://blog.tri-sen.com/tag/surge) - [recycle (4)](https://blog.tri-sen.com/tag/recycle) - [process protection (3)](https://blog.tri-sen.com/tag/process-protection) - [quench (3)](https://blog.tri-sen.com/tag/quench) - [refrigeration (3)](https://blog.tri-sen.com/tag/refrigeration) - ["Jim Jacoby (2)](https://blog.tri-sen.com/tag/jim-jacoby) - [PFD average (2)](https://blog.tri-sen.com/tag/pfd-average) - [PID (2)](https://blog.tri-sen.com/tag/pid) - [PID control (2)](https://blog.tri-sen.com/tag/pid-control) - [TMC (2)](https://blog.tri-sen.com/tag/tmc) - [process control (2)](https://blog.tri-sen.com/tag/process-control) - [safety systems (2)](https://blog.tri-sen.com/tag/safety-systems) - [turbine safety (2)](https://blog.tri-sen.com/tag/turbine-safety) - [turbomachinery controls (2)](https://blog.tri-sen.com/tag/turbomachinery-controls) - [API612 (1)](https://blog.tri-sen.com/tag/api612) - [API670 (1)](https://blog.tri-sen.com/tag/api670) - [MTTF (1)](https://blog.tri-sen.com/tag/mttf) - [PTI (1)](https://blog.tri-sen.com/tag/pti) - [TSODS (1)](https://blog.tri-sen.com/tag/tsods) - [axial compressor (1)](https://blog.tri-sen.com/tag/axial-compressor) - [compressor efficiency (1)](https://blog.tri-sen.com/tag/compressor-efficiency) - [hydraulic trip (1)](https://blog.tri-sen.com/tag/hydraulic-trip) - [incipient surge (1)](https://blog.tri-sen.com/tag/incipient-surge) - [overspeed detection (1)](https://blog.tri-sen.com/tag/overspeed-detection) - [polytropic (1)](https://blog.tri-sen.com/tag/polytropic) - [proof test interval (1)](https://blog.tri-sen.com/tag/proof-test-interval) - [stonewall (1)](https://blog.tri-sen.com/tag/stonewall) - [surge curve (1)](https://blog.tri-sen.com/tag/surge-curve) - [surge detection (1)](https://blog.tri-sen.com/tag/surge-detection) - [surge margin (1)](https://blog.tri-sen.com/tag/surge-margin) - [temperature control (1)](https://blog.tri-sen.com/tag/temperature-control) - [trip block (1)](https://blog.tri-sen.com/tag/trip-block) [See all](https://blog.tri-sen.com/deriving-the-universal-surge-curve#) ** HELP ###### HeadQuarters - North America  Engineering 109 Magellan Circle Webster, TX 77598 Tel:  +1-832-632-1211 Fax: +1 281-724-1226 ###### Netherlands Verlengde Zuiderloswal 4 Hilversum, NH 1216 BX Tel: [+31 88 011 9292](tel://+31%2088%20011%209292) ###### Singapore 56 Kallang Pudding Road #06-10 HH@Kallang  Singapore 349328 Tel: +65 6381 9188 Fax: +65 6381 9199 ### Search ** ### Stay in Touch - [** ** ](https://www.linkedin.com/company/tri-sen-systems-corporation/) [Privacy Policy](https://tri-sen.com/privacy) | [Terms and Conditions](https://tri-sen.com/terms) Copyright © 2019. Tri-Sen All rights reserved. Contact Us